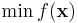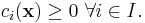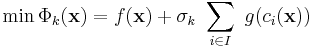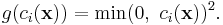Penalty method

Penalty methods are a certain class of algorithms for solving constrained optimization problems.

A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem. The unconstrained problems are formed by adding a term to the objective function that consists of a penalty parameter and a measure of violation of the constraints. The measure of violation is nonzero when the constraints are violated and is zero in the region where constraints are not violated.

Contents

Example

Let us say we are solving the following constrained problem:

\min f(\bold x)

subject to

c_i(\bold x) \ge 0 ~\forall i \in I.

This problem can be solved as a series of unconstrained minimization problems

\min \Phi_k (\bold x) = f (\bold x) %2B \sigma_k ~ \sum_{i\in I} ~ g(c_i(\bold x))

where

g(c_i(\bold x))=\min(0,~c_i(\bold x ))^2.

In the above equations, 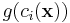g(c_i(\bold x)) is the penalty function while 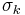\sigma_k are the penalty coefficients. In each iteration k of the method, we increase the penalty coefficient 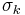\sigma_k (e.g. by a factor of 10), solve the unconstrained problem and use the solution as the initial guess for the next iteration. Solutions of the successive unconstrained problems will eventually converge to the solution of the original constrained problem.

Barrier methods

Barrier methods constitute an alternative class of algorithms for constrained optimization. These methods also add a penalty-like term to the objective function, but in this case the iterates are forced to remain interior to the feasible domain and the barrier is in place to bias the iterates to remain away from the boundary of the feasible region.

See also

References

Courant, R. Variational methods for the solution of problems of equilibrium and vibrations. Bull. Amer. Math. Soc., 49, 1–23, 1943.

Optimization: Algorithms, methods, and heuristics
Categories (Algorithms · Methods · Heuristics) · Software